A Calculated Approach to Astigmatism Management

Tun Kuan Yeo is a Consultant at the National Healthcare Group Eye Institute, Tan Tock Seng Hospital, Singapore. He graduated from University College London, UK, and is a Fellow of the Royal College of Ophthalmologists in the UK, and the Academy of Medicine, Singapore. Here, he explains how using toric formulae can help clinicians achieve the best results for patients with astigmatism.

An old problem

Astigmatism, first defined over two centuries ago, today affects 30-40 percent of patients. But modern cataract surgery provides an opportunity to reverse the associated visual acuity and contrast sensitivity issues. Astigmatism correction is particularly important for advanced lenses: its effect on distance and intermediate visual acuity may be worse with multifocal IOLs than with monofocal IOLs (1).

There are numerous strategies for correcting astigmatism: opposite clear corneal incisions, arcuate keratotomies (AKs), limbal relaxing incisions (LRIs), toric IOLs, corneal laser refractive surgery, femtosecond laser-assisted AKs, and femtosecond intrastromal astigmatic keratotomy. The weight of evidence favors toric IOLs: they give lower residual astigmatism, with lower standard deviation, than LRIs (2), and are more effective than LRIs in cases of higher astigmatism (3). Newer approaches, such as femtosecond AK, appear promising (4, 5), but may be inferior to toric IOLs with regard to standard deviation (6, 7). In brief, the toric IOLs are currently the most reliable and predictable strategy for astigmatism correction.

Nevertheless, a question remains: how can the toric IOL approach be optimized? Key success factors include accurate measurement of astigmatism; appropriate choice of toric formula; incorporation of personalized surgically induced astigmatism (SIA); and good IOL alignment and rotational stability.

Astigmatism measurement today is assisted by an abundance of instruments and technologies. Some (Scheimpflug, colored LEDs, and swept-source OCT) measure both anterior and posterior corneal astigmatism (PCA), thereby providing a value for total corneal astigmatism. Since standard keratometry only measures anterior corneal astigmatism, the above technologies might be expected to provide better outcomes. However at present, we find that using predicted PCA with advanced toric formulae is still more accurate than measuring total corneal astigmatism.

So which toric formula should we select? Again, today’s ophthalmologist is spoiled for choice. Recent years have seen the field evolve from fixed ratio formulae to ELP-based formulae, and then to PCA/ ELP-based formulae (see Toric formulae). The major recent driver of change was Koch’s demonstration of the importance of PCA (8); his findings show that we must account for PCA if we are to derive a correct value for total astigmatism. This new understanding led to approaches such as the Baylor nomogram; the Barrett Toric formula (9), the Abulafia-Koch regression formula (10), and the J&J Vision toric regression formula (11). In choosing and applying a given formula, we should not forget the importance of surgically-induced astigmatism (SIA). In particular, remember that mean SIA is only the average of the magnitudes of induced astigmatism, whereas centroid SIA is the vector average of induced astigmatism, so includes both magnitude and direction. Centroid SIA is therefore the more accurate value to utilize.

Of course, a toric IOL will perform poorly if it is incorrectly positioned during surgery or rotates post-surgery. A misalignment of 10 degrees is estimated to result in a ~33 percent reduction in toric efficacy; use manual markings or electronic axis guidance systems with care. Rotational stability subsequent to insertion is generally influenced by IOL design (careful IOL choice can provide outcomes of 95 percent within 5 degrees of target).

New calculations

Recently, I developed the Emmetropia Verifying Optical (EVO) formula (12, 13); version 1.0 was created in 2016, and updated to version 2.0 in 2019.

The EVO formula predicts IOL power with up to five parameters (axial length, K, ACD, LT and CCT). For toric calculations, it predicts both PCA and angle alpha, and also accounts for different toric IOL surfaces – anterior, posterior or bitoric – by modulating the principal planes according to location and power of the toric surface. For example, the online EVO Toric input page (12) permits selection of the Bausch + Lomb enVista® IOL’s unique toric steps (1.25, 2.00, 2.75, 3.50, 4.25, 5.00 and 5.75).

A 13,000-eye study (14) showed that version 1.0 of the EVO formula giving spherical equivalent prediction outcomes similar to the Barrett Universal II and better than the Hill-RBF 2.0, Holladay I, Haigis, Holladay II, SRK/T and Hoffer Q formulae. Application of EVO version 2.0 to a dataset of 1079 eyes (15) showed that it provided the lowest mean absolute error, lower standard deviation, and highest percentage of outcomes within 0.5 diopters than nine other formulae. Similarly, a recent 150 eye comparison of 15 formulae showed that EVO formula had the lowest standard deviation and lowest mean absolute error, and highest percentage outcome within 0.5 diopters (16). For toric predictions, our own comparison (17) of five formulae in 117 eyes showed that the EVO Toric formula gave lower mean absolute error and higher percentages within 0.5 D (80.34 percent) compared to the Barrett Toric formula, Abulafia-Koch regression, Johnson & Johnson Vision online calculator, and Holladay I Toric formula.

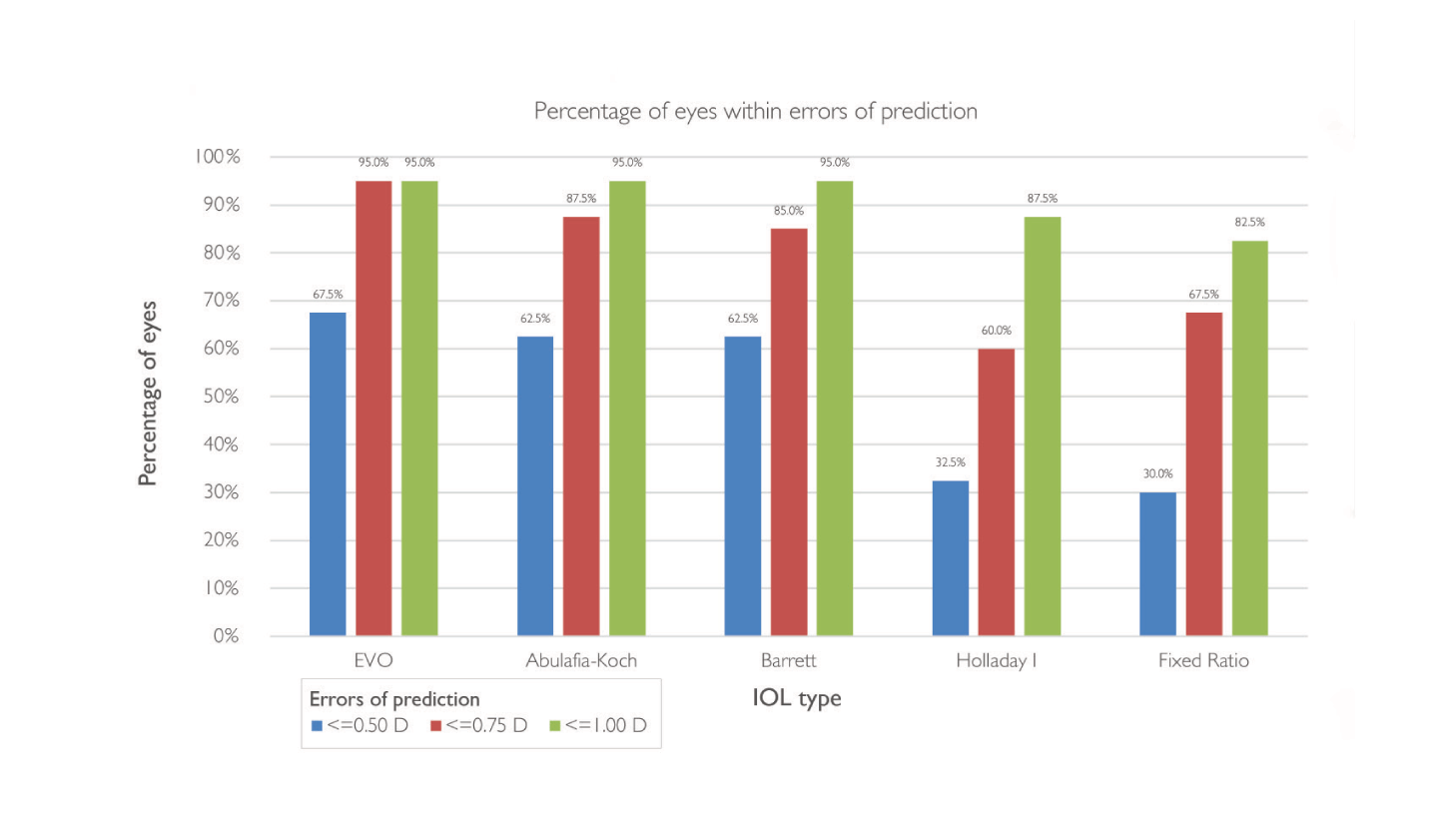
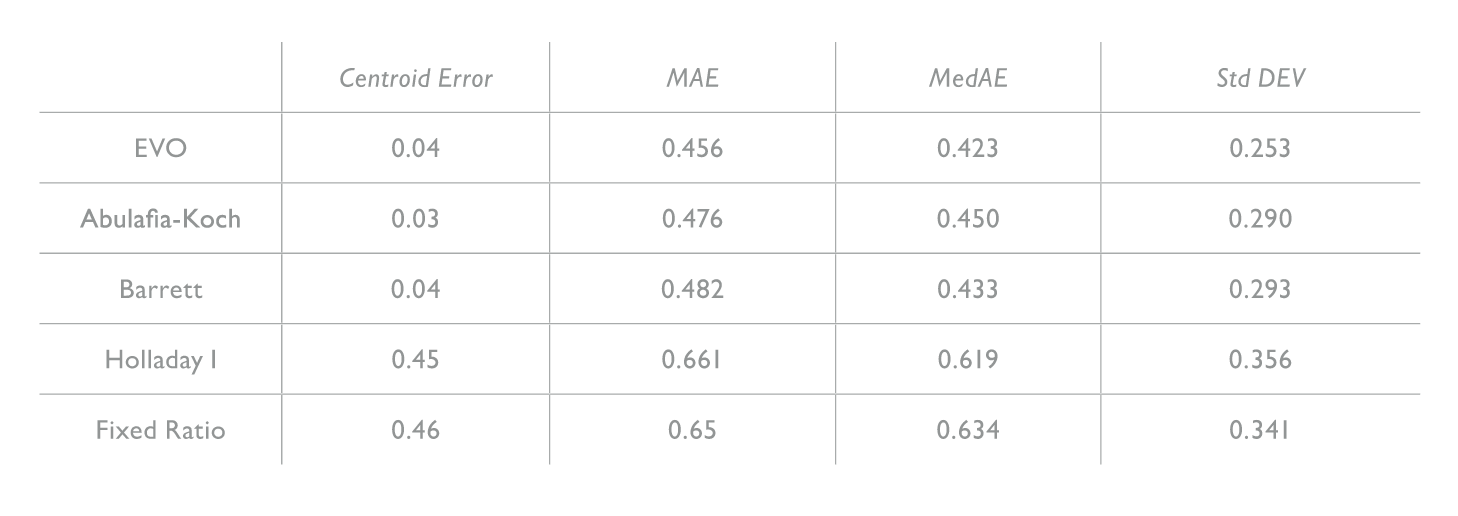
Finally, we demonstrated compatibility of EVO Toric formula with the enVista® IOL MX60T. The study (see The enVista study: Outline) included a broad range of axial lengths and K values, and the full range of enVista toricities. The EVO ToricenVista® combination provided statistically significant reductions in cylinder and gave higher percentages of astigmatic correction within 0.5 D of target than Abulafia-Koch and Barrett. Similarly, with regard to spherical equivalent outcomes, EVO provided the lowest mean absolute error (0.305) and median absolute error (0.203). This was followed by Barrett (0.311 and 0.243, respectively) and Haigis (0.323 and 0.300, respectively). In light of these results, I recently collaborated with Bausch + Lomb to develop a new online Toric IOL calculator that employs the EVO Toric algorithm to help surgeons properly fit the company’s toric lenses for their patients.

• Single surgeon
• 40 eyes
• enVista® MX60T IOL
• Spherical comparison formulae:
                • Barrett, EVO, Haigis, Hoffer Q, Holladay I, SRK/T
• Toric comparison formulae:
                • Abulafia-Koch regression, Barrett Toric, EVO Toric, Holladay I, Fixed ratio
• Mean age: 70.9
• Female:male 26:14
• Mean axial length: 24.03 mm (range 21.48–27.38 mm)
• Mean K: 44.44 D (range 42.03–46.88 D)
• Mean IOL power: 19.14 D (range +7–+28 D)
• Mean toric power: 3.16 D (range 1.25–5.25 D)

Conclusions

Toric IOLs remain the most reliable meansof correcting astigmatism during cataract surgery. Optimal IOL outcomes require attention to PCA and SIA; note that current predicted PCA values, are still more reliable than available measured PCA values. Finally, recent data shows that the EVO Toric formula – for example, in conjunction with the enVista® MX60T toric IOL – provides outcomes equivalent to or better than standard posterior corneal astigmatism formulae.